如何使用戴维宁定理

了解如何使用戴维宁定理计算线性电路中负载电阻两端的电流和电压。

如何使用戴维宁定理计算负载电流和电压保持简单

有多种方法可用于分析复杂的电路。这些包括网格分析、节点分析或基尔霍夫电路定律。问题是，当你设计直流电源网络时，负载的值会随着设计过程的展开而改变。不必在每次负载变化时重新计算整个电路的电流和电压，你可以使用戴维南定理简化此过程。在此文中，我们将研究如何将任何复杂的线性电路简化为单个电压源和串联电阻。从那里，我们可以使用戴维宁等效电路来快速计算我们的电流和电压。

什么是戴维宁定理？

与所有其他数学和科学理论/定律一样，戴维宁定理是由莱昂·查尔斯·戴维宁 ( Léon Charles Thévenin ) 本人发明的。Thévenin是一名法国电报工程师，出生于法国莫城。在电报工程师团工作后，他于 1882 年被任命为École supérieure de télégraphie的教学督导。正是在这里，他对电路测量产生了兴趣。当时，他使用了两种可用的方法--基尔霍夫电路定律和欧姆定律。

为了让每个工程师都能更轻松地进行复杂的电路分析，戴维宁开发了他现在著名的戴维宁定理。 该定理将复杂电路简化为简化的戴维宁等效电路。

该定理指出，你可以采用任何包含多个电动势和电阻元件的线性电路，并将电路简化为一个电压源和连接到负载的串联电阻。

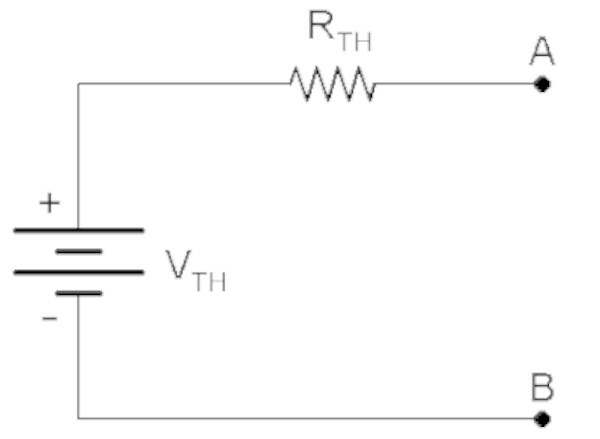
为什么要使用戴维宁定理？

在这种情况下，线性电路是一种包含无源元件（如电阻器、电感器和电容器）的电路。但是，如果你使用的电路包含气体放电或半导体元件，那么你的电路就是非线性电路。这不是戴维宁定理适用的。那么为什么要用这个定理进行线性电路分析呢？

效率：戴维宁定理提供了一种分析电源电路的简单方法，通常在分析过程中负载会改变值。该定理提供了一种计算流过负载的电压和电流的有效方法，而无需重新计算整个电路。

专注：戴维宁定理还提供了一种有效的方法，可以将你的分析重点放在电路的特定部分。这使你可以通过使用戴维宁等效电路简化其余电路来计算特定端子的电压和电流。

例如，检查下面的电路。这里我们有电阻 R2 作为我们的负载。我们希望计算流过该电阻的电压和电流，而不必每次负载电阻值发生变化时都使用像 Branch Current、Mesh Current 等耗时的分析方法。

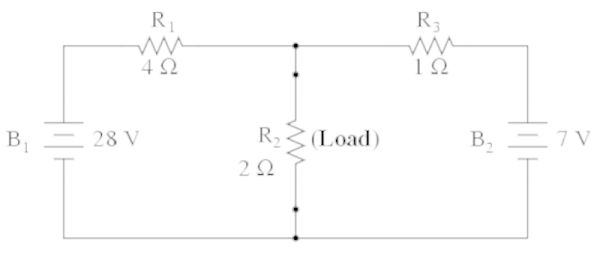
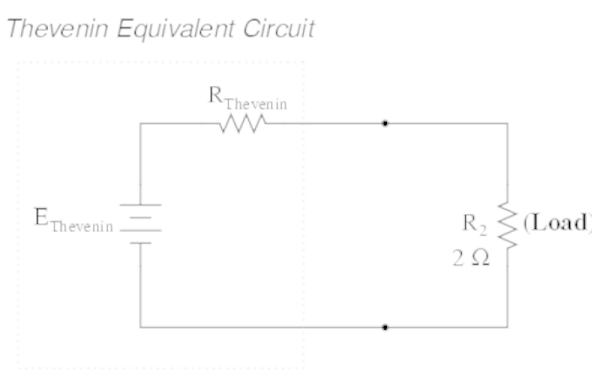
为了简化这一过程，我们可以使用戴维宁定理来消除负载电阻和电压。然后我们将电路的其余部分简化为单个电压源和串联电阻。在这个简化的戴维宁电路中，两个电阻器 R1 和 R3 以及次级电压 B2 都被简化为单个电压源和串联电阻。就负载电阻而言，简化的电压和电阻将与我们的原始电路相同。现在我们只有两个简单的变量可以在我们的计算中使用。

戴维宁定理在行动

让我们看一个示例电路并计算流过两个端子之间负载电阻的电流。使用戴维宁定理分析直流电路的过程需要以下步骤：

通过移除所有电压源和负载电阻来找到戴维宁电阻。

通过插入电压找到戴维宁电压。

使用 Thevenin Resistance and Voltage 找出流过负载的电流。

这是我们将要使用的示例电路：

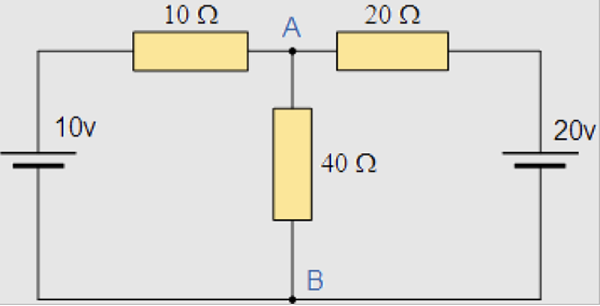
步骤 1 – 戴维宁抵抗

我们首先需要移除连接端子 A 和 B 的 40 欧姆负载电阻以及所有电压源。这样做将为我们提供零伏的开路，只剩下两个串联的电阻器。

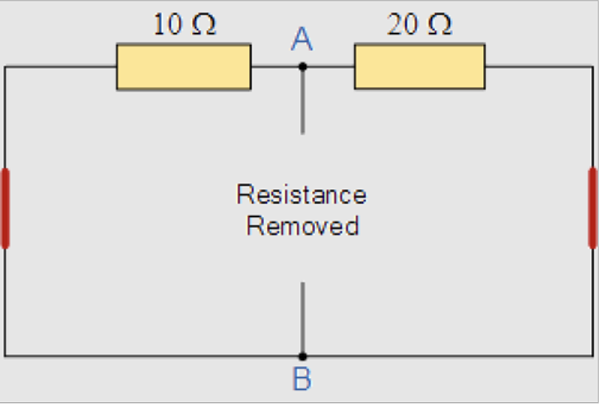
要计算总戴维宁阻力，我们可以使用以下过程：

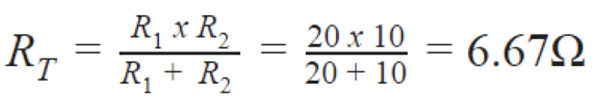
第 2 步 – 戴维宁电压

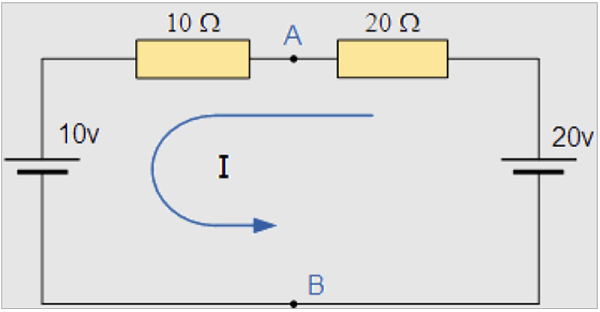
然后我们可以使用欧姆定律来计算流过电路的总电流：

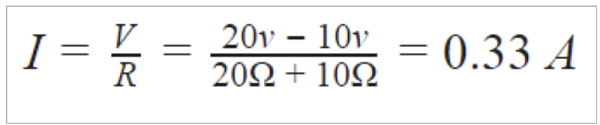
由于这些电阻串联，它们将共享相同的 0.33 安培。我们可以使用这些电阻值和我们的电流来计算压降，即：

第 3 步 – 负载电流

现在我们有了戴维宁电阻和电压，我们可以将戴维宁等效电路与原始负载电阻放在一起，如下所示：

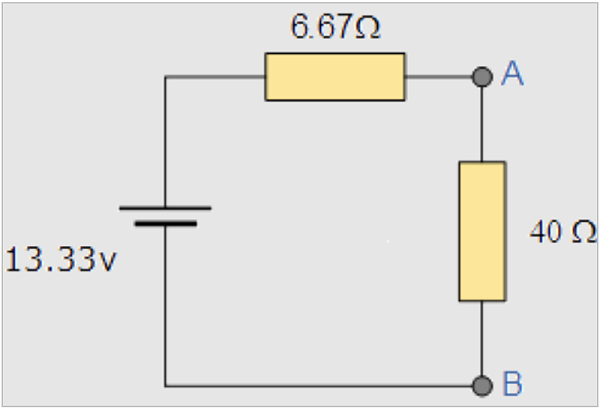
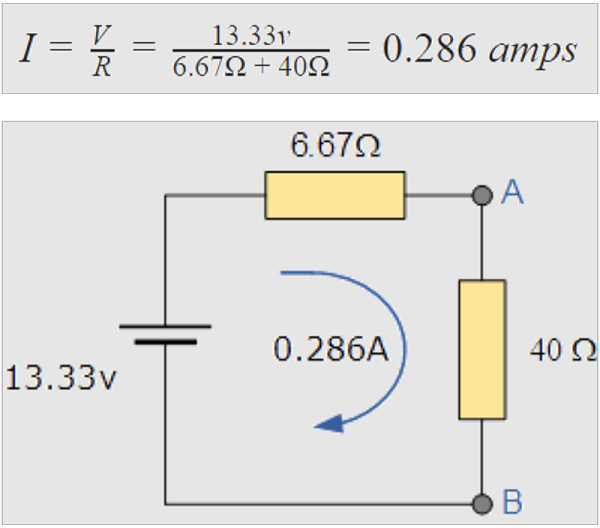
从这里，我们可以使用欧姆定律来计算流过负载电阻的总电流，如下所示：

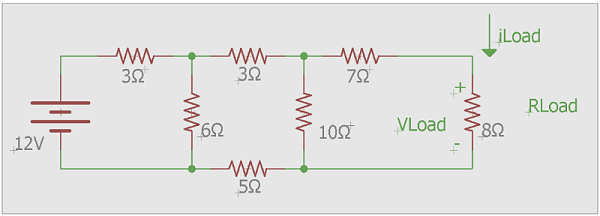
使用戴维南定理找出下面电路的 i负载和 v负载

记住三步过程：

通过移除所有电压源和负载来找到戴维宁电阻。

通过重新连接电压源找到戴维宁电压。

使用 Thevenin Resistance and Voltage 找出流过负载的总电流。

把事情简单化

计划设计直流电源电路？你可能会加入一个负载，其值会在电路分析期间发生变化。不必在每次更改此负载值时都重新计算整个电路，现在有了戴维南定理，你的工作就变得轻松了。

该定理允许你采用具有各种电阻元件和 EMF 的任何复杂线性电路，并将其简化为戴维宁等效电路。使用这个简化的电路，您可以轻松计算流过负载的总电流和电压。对于需要高效分析电源设计和其他复杂应用电路的任何工程师来说，这可以节省大量时间。

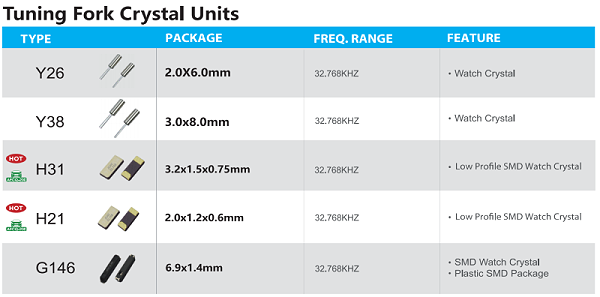
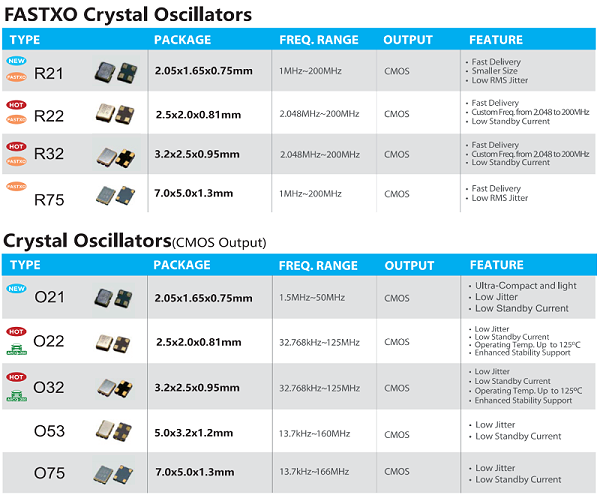
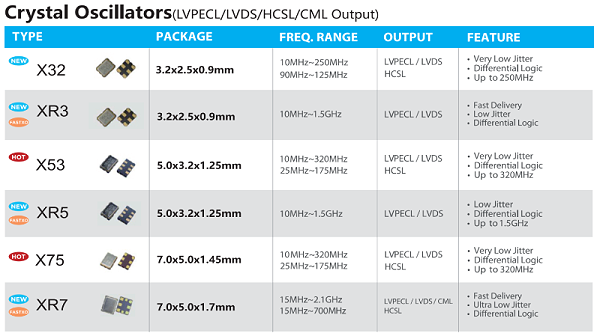
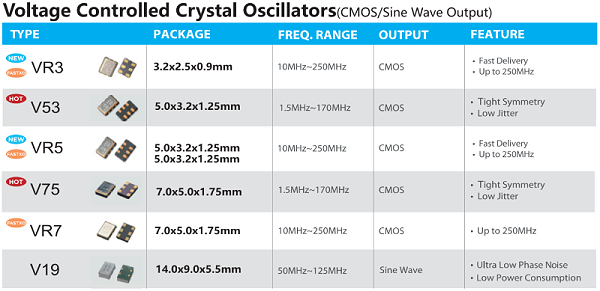
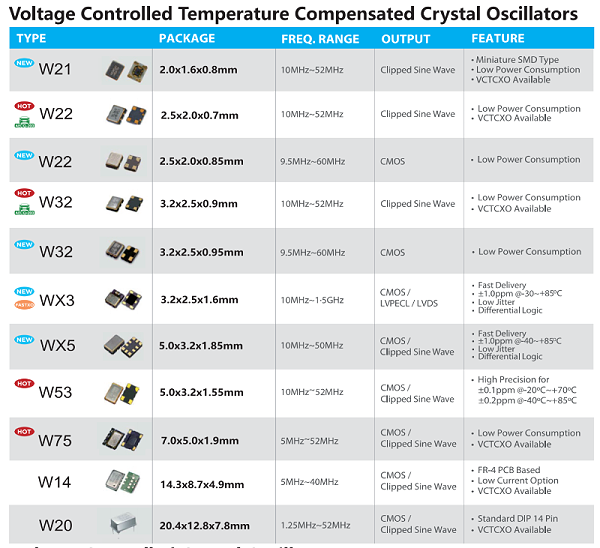
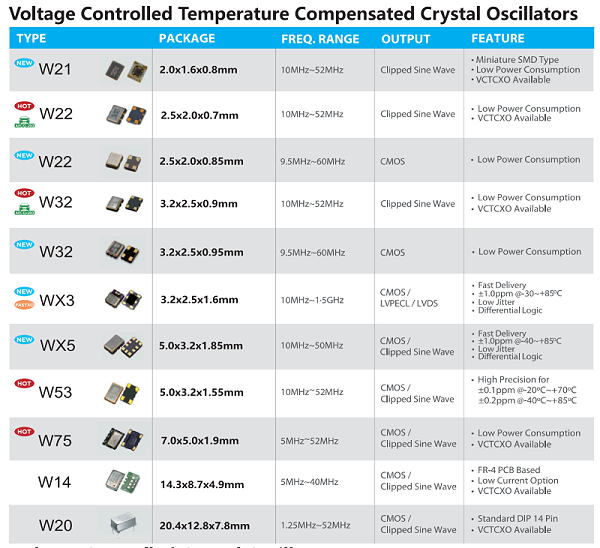
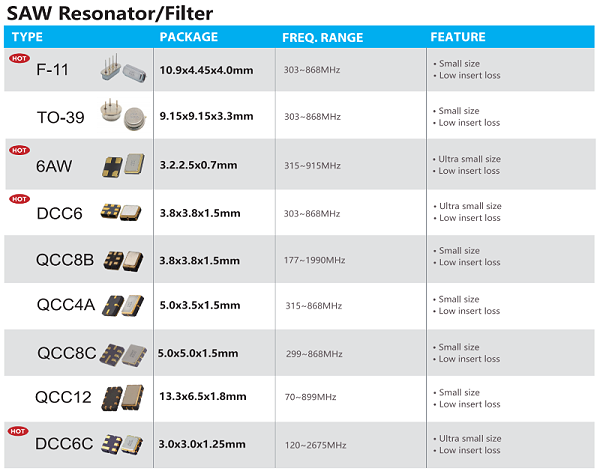
深圳市晶光华电子有限公司 专注石英晶振生产26年，强大的专业团队，服务超过上千家客户，高品质， 年产能6亿PCS，帮助客户选型，免费匹配及测试，交付快；如果您对我们的石英晶振感兴趣，欢迎咨询我们的客服，获取详细资料及报价，我们将为您提供专业贴心的服务。